Vaikai turi pastebėti ir aptarti, kas sieja kiekvienos dėžutės sagas. Požymiais galime laikyti sagų dydį, spalvą, formą, akučių skaičių. Pirmoje dėžutėje visos sagos apvalios, jų pririnktume iš viso 11. Antroje dėžutėje sagos kvadrato arba stačiakampio formos, iš viso jų yra 9. Trečioje dėžutėje visos sagos ovalios – jų 5.
Taigi sagos dėžutėse surūšiuotos pagal formą. Jei vaikas kitaip rūšiavo, reikia išklausyti, kodėl jis taip darė, prašyti argumentuoti.
Taigi sagos dėžutėse surūšiuotos pagal formą. Jei vaikas kitaip rūšiavo, reikia išklausyti, kodėl jis taip darė, prašyti argumentuoti.
2. Eglutės žaisliukai
Sprendžiamas atvirkštinis rūšiavimui uždavinys: reikia įsiginti, kas ir kaip surūšiuota (apvalūs ir pailgi raštuoti objektai, žvaigždės ir snaigės), o tada nustatyti, ar yra netinkamų objektų. Į jokią dėžutę negalime įdėti 3 žaisliukų: namelio, kubelio ir trikampio žaisliuko.
3. Nežemiški gyventojai
Vaikai turi aptarti, pagal ką galėtume atpažinti, kas kurioje planetoje gyvena. Tai galėtų būti padarėlių spalva ir forma. Gal vaikai sugalvotų dar kokių požymių. Svarbiausia, pateikti argumentus, logiškai pagrįsti. Kiekvieno padarėlio galvos forma vienareikšmiškai atitinka kurios nors planetos formą.
4. Batai ir jų raišteliai
Nustatome požymius, pagal kuriuos galėtume parinkti batų raištelius: tai raištelių ilgis, plotis, spalva, na dar galėtų būti funkcionalumas. Šiame uždavinyje tinka visi kriterijai. Vaikai galėtų aptarti, kuris kriterijų svarbiausias. Tarkime, raištelių ilgis. Spalvos parinkimas labiau individualus. Raištelio plotis taip pat svarbus, jei mažos skylutės, tiesiog galima neįverti. Funkcionalumą galima aptarti paskutiniu raišteliu, kuris yra su burbuliukais – tokie raišteliai gaminami, jie patogūs bėgimo, sportiniuose batuose, nes neatsiriša.
1 – C. 2 – B. 3 – D. 4 – A.
1 – C. 2 – B. 3 – D. 4 – A.
5. Antspaudų piešinys
Pirmiausia dedamas tas antspaudas, kuris turi būti apačioje – tai yra debesis. Antrasis nuo apačios objektas yra Žemė, paskui – žmogeliukas ir paskiausiai raketa. Raketą sudaro dvi dalys, reikia pastebėti, kad viršutinė dalis įsikiša į apatinę. Vadinasi, pirma antspauduojama viršutinė dalis, po to – apatinė.
3–5–4–1–2
3–5–4–1–2
6. Sluoksninis piešinys
Pirmiausia dedamas tas antspaudas, kuris turi būti apačioje – tai yra tvenkinys. Antrasis nuo apačios objektas yra medis, po to iš eilės antspauduojama vėliava, uola, krūmas ir paskiausiai bebras.
6–2–5–4–3–1
6–2–5–4–3–1
7. Ieškok ir analizuok
Pirmiausia reikia surasti kiek galima daugiau paslėptų žodžių ir tada dėlioti iš jų sakinį.
PO LELIJOS LAPU TUPI ŽALIA VARLĖ IR KVAKSI
Vaikai gali gauti ir kitokią žodžių tvarką sakinyje. Turėtų būti aišku, kad žodžių linksnių negalima keisti (jei nepasakyta, vadinasi, reikia imti žodžius, kaip jie duoti).
PO LELIJOS LAPU TUPI ŽALIA VARLĖ IR KVAKSI
Vaikai gali gauti ir kitokią žodžių tvarką sakinyje. Turėtų būti aišku, kad žodžių linksnių negalima keisti (jei nepasakyta, vadinasi, reikia imti žodžius, kaip jie duoti).
8. Įdėmiai ieškok
Uždavinys reikalauja atidumo. Skaičiai įkomponuoti į foną, pasvirę ar paguldyti. Kai kada vaikai gali pamatyti tik vieną skaitmenį, pavyzdžiui, 1 vietoj 13 (tolimesnės varlės akys). Radus dar vieną vienetą, teks grįžti ir tikrinti. Trūksta šių skaičių: 10, 11, 18, 19
9. Vėliavėlės
Į akis turėtų kristi violetinės vėliavėlės – jos eina po dvi. Taip pat ir trikampės vėliavėlės vis kabinamos po dvi. Tarp šių porų yra viena stačiakampė vėliavėlė, kuri kabo paskutine eilėje, vadinasi, toliau reikia kabinti trikampę vėliavėlę:

10. Juostelės
Jei juostelės imsi ieškoti nuo vienos ar kito galo, lengvai įsitikinsi, kad gali atkirpti 4 vienodas juosteles. Jei imtum kirpti iš vidurio, tuomet juostelių išeitų mažiau. Norint įsitikinti, ar sprendimas teisingas, tai yra, ar rasta daugiausia vienodų juostelių, reikia patikrinti visus galimus kirpimus ir tada išrinkti didžiausią.
11. Plunksnos
Kadangi plunksnos net keturių spalvų, tai pastebėti jų išsidėstymo dėsningumą nėra lengva. Vis tik jei gerai pagalvotume, pastebėtume, yra dvi poros raudonų ir dvi poros geltonų plunksnų. Taigi pamestos raudona ir geltona plunksnos, o jas niekaip kitaip negalime įdėti kaip į 1 i 2 numeriu pažymėtas vietas. Na ir beliko įdėti žalią plunksną 3 numeriu pažymėtoje vietoje. Vadinasi, plunksnos kartojasi pagal šabloną: raudona, raudona, žalia, geltona, geltona.
1–D; 2–A; 3–C.
1–D; 2–A; 3–C.
12. Karoliai bebriukei
Karoliams turi galioti abi sąlygos. Pradedame tikrinti kurią nors vieną sąlygą, tarkime, pirmąją. Atkrenta tik vieni karoliai: B atveju viena šermukšnių uoga yra ne tarp pušų spyglių. Toliau reikia skaičiuoti obuolių sėklas ir spyglius. D atveju galima neskaičiuoti (nes daug), o tiesiog lyginti sėkla – spyglys ir matome, kad vienu spygliu daugiau.
Teisingas A.
Teisingas A.
13. Bebro gimtadienis
Ant torto dvi uždegtos ir dvi neuždegtos žvalutės, užrašę tai dvejetainiais skaitmenimis, gautume 1100. Paieškoję pateiktoje lentelėje, rastume, kad šis skaičius atitinka 12, tai yra bebrui 12 metų.
14. Informatiko Naujieji metai
Švenčiami 2017-ieji metai, nes 0010 yra 2, 0000 yra 0, 0001 yra 1, 0111 yra 7.
15. Rytmetis
4 paveikslėlis yra netinkamoje vietoje, nes pirma reikėtų nusiprausti, o paskui rengtis..


16. Grįžus iš mokyklos
Labiausiai tinka paveikslėlis B, nes Gabrielė turėtų paruošti pamokas.


17. Spalvotas bokštas
Žiedus reikia mauti pagal taisykles, t. y. pagal nurodytą spalvų seką: raudona, žalia, geltona. Iš esamų diskų galima sudaryti 3 sekas (yra po tris kiekvienos spalvos žiedus), viena seka jau užmauta, vadinasi, vykdant nurodytas taisykles bokštą sudarys 12 žiedų.
18. Pomidorai
Paprasčiausias sprendimas – patikrinti visus atvejus, sakoma, visiškas galimybių perrinkimas. Tai yra pradedame pirmuoju krūmu ir skaičiuojame nuskintų pomidorų skaičių, tada pradedame antruoju krūmu ir vėl skaičiuojame pomidorus ir taip darome, kol išbandome visus šešis krūmus. Tada palyginame kiekvienu atveju gautų nuskintų pomidorų skaičius ir pasirenkame didžiausią – turime pradėti nuo 4-ojo krūmo ir nuskintume 7 pomidorus.
Jei pomidorų būtų daug, toks sprendimo būdas reikalautų daug laiko. Reikėtų ieškoti geresnio sprendimo būdo. Pavyzdžiui, galima įvertinti, kiek iš viso pomidorų yra ant nelyginių krūmų (8) ir lyginių (9). Taip pat galima įvertinti, kur mažiausiai pomidorų: ant 5-ojo krūmo tik vienas pomidoras, vadinasi, einant nelyginiais numeriais robotas nebegalės padaryti antro rato. Šitaip samprotaujant prieiname išvados, kad reikia tikrinti lyginius krūmus ir pradėti nuo krūmo, turinčio daugiausia pomidorų (kodėl?).
Jei pomidorų būtų daug, toks sprendimo būdas reikalautų daug laiko. Reikėtų ieškoti geresnio sprendimo būdo. Pavyzdžiui, galima įvertinti, kiek iš viso pomidorų yra ant nelyginių krūmų (8) ir lyginių (9). Taip pat galima įvertinti, kur mažiausiai pomidorų: ant 5-ojo krūmo tik vienas pomidoras, vadinasi, einant nelyginiais numeriais robotas nebegalės padaryti antro rato. Šitaip samprotaujant prieiname išvados, kad reikia tikrinti lyginius krūmus ir pradėti nuo krūmo, turinčio daugiausia pomidorų (kodėl?).
19. Skaityk ratu
Uždavinys reikalauja tiksliai įvykdyti aprašytą algoritmą. Pradžioje gali būti sunku pasirinkti, kuria kryptimi skaityti: raudona rodyklė rodo, kad ratas sukamas pagal laikrodžio rodyklę, tačiau skaityti raides reikia priešinga kryptimi!
B I B L I O T E K A
B I B L I O T E K A
20. Ieškok klaidos
Uždavinys reikalauja tiksliai įvykdyti aprašytą algoritmą. Pradžioje gali būti sunku pasirinkti, kuria kryptimi skaityti: raudona rodyklė rodo, kad ratas sukamas pagal laikrodžio rodyklę, tačiau skaityti raides reikia priešinga kryptimi! Vykdydami algoritmą, turime stebėti, kur atsiranda klaida. Pagal algoritmą perskaitome: S E K M A D I ir štai tada matome, kad praleidę 7 langelius, gautume vėl raidę I, kas negali būti! Vadinasi, klaida čia – vietoj 7 langelių praleisi 6. Teisingas žodis turėtų būti: SEKMADIENIS
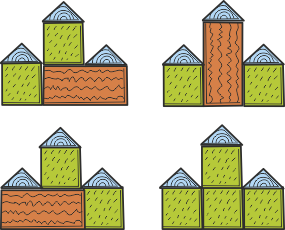
21. Pilies paveikslas
Galime sudėlioti 4 skirtingais būdais. Sprendimas pateiktas piešiniais, panagrinėkite:

22. Monetos
Galime spręsti bent dviem būdais: rankioti monetas (skaičius) ir iš jų sudaryti reikiamą sumą (10) arba imti skaičių 10 ir išskaidyti jį naudojant skaitmenis 1, 2 ir 5 visais įmanomais būdais. Bet kuriuo atveju perrinkimas turi būti atliekamas sistemingai, pavyzdžiui, imame didžiausią skaičių 5 ir toliau pridedame kitus. Gauname 4 būdus (būtina įsitikinti, kad yra reikiamo nominalo monetų):
5+5; 5+2+2+1; 2+2+2+2+2; 2+2+2+2+1+1
5+5; 5+2+2+1; 2+2+2+2+2; 2+2+2+2+1+1
23. Pasirink pietus
Galima spręsti bent dviem skirtingais būdais: imti kiekvieną rinkinį ir nuosekliai tikrinti pagal schemą arba, antras būdas, imti schemą, eiti jos šakomis ir stebėti, ar visi pateikti rinkiniai tinka. Spręskime antruoju būdu. Viršūnėje yra padėklas – visi rinkiniai jį turi. Antras lygmuo – sriubos: žirnienė, sultinys, šaltibarščiai, visi rinkiniai turi po kurią nors iš sriubų. Trečio lygmens patiekalai irgi yra visuose rinkiniuose, tačiau čia jau reikia žiūrėti, ar jie padėti ten, kur reikia – iš tiesų jau turime taikyti pirmąjį sprendimo būdą, tikrinti pateiktus rinkinius. Štai čia ir pastebime, kad pasirinkus žirnienę, cepelinų negalime imti, vadinasi, rinkinys C neatitinka taisyklių.
24. Perskaityk žodžius
Žodžius skaitome naudodamiesi medžiu: pradedame nuo aukščiausios medžio viršūnės (M raidė) ir tada leidžiamės šakomis žemyn. Medis dvejetainis taisyklingas: iš kiekvienos viršūnės išeina po dvi šakas ir yra keturi lygiai, vadinasi, visi žodžiai iš keturių raidžių. Svarbiausia – nusistatyti tvarką, kaip eisime medžio šakomis, kad nepraleistume kurio nors žodžio. Pavyzdžiui, leisdamiesi žemyn kiekvienoje viršūnėje galime pirma imti kairiąją šaką, po to, kai kairiosios išnaudotos, imti dešiniąsias. Taip rasime, kad trūksta žodžio MENĖ.
25. Vabaliukas robotukas
Šiame uždavinyje galima ne visai vienodai suprasti pasakymą „einama per vieną langelį“, „einama per du langelius“ ir t. t. Kas žaidžia stalo žaidimus, tai supras, kad paeiti per vieną langelį, reiškia, atsistoti į gretimą langelį. Tačiau galima galvoti ir kitaip, būtent, kad reikia praleisti (peršokti) vieną langelį ir atsistoti į vienu toliau. Labai dažnai aprašant algoritmus žodžiais gaunami netikslumai, dviprasmybės. Dėl to kompiuteriams algoritmai pateikiami griežtai sutartomis programavimo kalbos komandomis. Kaip elgtis šiuo atveju? Galima spręsti interpretuojant sąlygą ir vienu, ir kitu būdu, ir gauti du sprendimus. Atidžiau apžiūrėję lentą, viename langelyje pastebime tris rodykles: jei peršoktume per tris langelius, tai išeitume už lentos ribų, vargu, ar uždavinio autoriai to norėtų. Todėl sutarkime, kad pasakymas „einama per du langelius“ reiškia atsistoti antrame langelyje. Analogiškai su kitu langelių skaičiumi.
Reikia išnagrinėti visus atvejus, tai yra pradėti iš visų keturių įėjimų.
Pradėjęs iš pirmojo, robotukas atsiduria trečiame langelyje, o iš ten dvi rodyklės vėl veda į pirmąjį – gaunamas amžinasis ciklas.
Pradėjęs iš antrojo langelio, robotukas padarys didelį ratą lentoje ir pagaliau pasieks finišą.
Trečiasis įėjimas po keturių žingsnių atsiduria į vieną iš pirmojo įėjimo kelio langelių, vadinasi, gaunamas amžinasis ciklas.
Ketvirtasis įėjimas jau antruoju žingsniu pataiko į vieną iš antrojo įėjimo kelio langelių, vadinasi, finišas bus pasiektas.
Visus kelius pavaizduosime paveikslais (raudona linija).
Taigi robotukas finišą pasieks pradėjęs iš 2-ojo ir 4-ojo įėjimų.
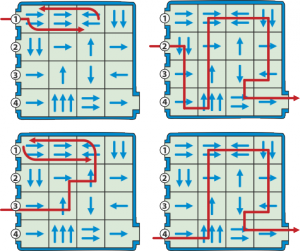
Reikia išnagrinėti visus atvejus, tai yra pradėti iš visų keturių įėjimų.
Pradėjęs iš pirmojo, robotukas atsiduria trečiame langelyje, o iš ten dvi rodyklės vėl veda į pirmąjį – gaunamas amžinasis ciklas.
Pradėjęs iš antrojo langelio, robotukas padarys didelį ratą lentoje ir pagaliau pasieks finišą.
Trečiasis įėjimas po keturių žingsnių atsiduria į vieną iš pirmojo įėjimo kelio langelių, vadinasi, gaunamas amžinasis ciklas.
Ketvirtasis įėjimas jau antruoju žingsniu pataiko į vieną iš antrojo įėjimo kelio langelių, vadinasi, finišas bus pasiektas.
Visus kelius pavaizduosime paveikslais (raudona linija).
Taigi robotukas finišą pasieks pradėjęs iš 2-ojo ir 4-ojo įėjimų.

26. Katinas ir pelė
Pasakymą „einama per vieną langelį“ supraskime, kad paeiname į gretimą langelį (kaip ir 25-ame uždavinyje). Analogiškai ir su kitu langelių skaičiumi.
Reikia atidžiai sekti katino ir pelės ėjimus, nepamirškime, kad katinas pradeda ir ėjimai daromi paeiliui. Galima pasiimti du žaidimo kauliukus ir praktiškai atlikti ėjimus. Pamatysime, kad ir katinas, ir pelė eina ratais (amžinieji ciklai) ir jie negali susitikti, nes vis eina vienas paskui kitą. Vadinasi, pelei pavyks pabėgti.
Katino kelias pavaizduotas raudona linija, pelės – juoda.
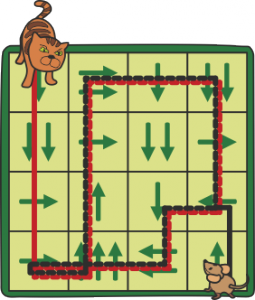
Reikia atidžiai sekti katino ir pelės ėjimus, nepamirškime, kad katinas pradeda ir ėjimai daromi paeiliui. Galima pasiimti du žaidimo kauliukus ir praktiškai atlikti ėjimus. Pamatysime, kad ir katinas, ir pelė eina ratais (amžinieji ciklai) ir jie negali susitikti, nes vis eina vienas paskui kitą. Vadinasi, pelei pavyks pabėgti.
Katino kelias pavaizduotas raudona linija, pelės – juoda.

27. Roboto mašina
Roboto valdoma mašina pirmiausia važiuoja vieno ilgio atkarpą, tai atliekama komanda priekin 1, vadinasi, tinka tik A ir D atvejai. Toliau reikia nuspręsti, kur sukti: kairėn ar dešinėn – reikia įsivaizduoti save vairuotojo vietoje, taigi turime sukti dešinėn. Tada tinka tik D atvejis. Toliau reikia įsitikinti, ar tikrai jis tinka, tai yra ar parašytos komandos nuves į Bebriją. Tikrai taip.
28. Robotas ir sausainiai
Šioje užduotyje svarbu nesupainioti, jog pirmas padėtas sausainis bus apačioje, o ne viršuje. Teisingas atsakymas yra A, nes pagal komandų seką gauname: kvadratas, kvadratas, skritulys, trikampis, skritulys.
29. Kelių pasirinkimas
Pirmiausia išsiaiškiname nagrinėdami traukinius: matome, kad pirmoje sankryžoje reikia sukti į kairę, o antroje – į dešinę. Tada reikia rasti legendą (lentelė kairėje viršuje) ir išsiaiškinti, ką žymi a ir b sąlygos: a reiškia posūkį į dešinę, b – į kairę. Vadinasi, atsakymas B.
30. Robotas neša
Kadangi krovinys sunkesnis už 10 kg, tai kiekviename aukšte robotui reikės 2+1 minutės. Užduoties sąlyga suformuluota taip, kad galima diskutuoti dėl pradžioje sugaištamos 1 minutės ruošimuisi: ar jos reikia cokoliniame aukšte (prieš pakylant į pirmąjį aukštą), ar ne. Nuo to priklauso atsakymas: 8 arba 9 minutės.
31. Kas antras posūkis
Reikia laikytis abiejų algoritmo taisyklių: eiti tiesiai ir sukti į kas antrą posūkį. Katinas nukeliaus į D (pavaizduota paveiksle).
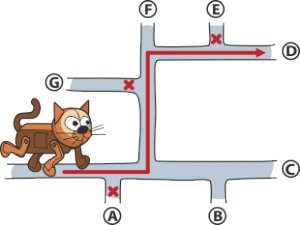

32. Plaukiojantis robotukas
Reikia atidžiai vykdyti, kas paliepta: plaukti tiesiai, priplaukus posūkį, sukti kairėn. Jei teisingai atliksime, pateksime atgal į tvenkinį A. Čia sąlygą galime interpretuoti dvejotai: robotukas plaukia tiesiai, kol atsitrenkia į sieną; arba, kita versija: robotas išplaukia iš tvenkinio ir vėl pradeda plaukti iš pradžių.
33. Judėjimas įstrižai
Reikia pereiti nuo pradžių katino kelią ir skaičiuoti posūkius (kad teisingai pasisuktume, reikia sekti katino žiūrėjimo kryptį). Katinas pasisuks septynis kartus šitaip: dešinėn, kairėn, kairėn, dešinėn, dešinėn, kairėn, kairėn. Kaip matome, katinas į kairę pasisuks keturis kartus, vadinasi, ten buvo pelės – katinas turėjo suėsti 4 peles.
34. Akmenukai
Robotas turi vykdyti aprašytą algoritmą – taisykles, kada imti akmenuką ir per kiek langelių žengti. Po vieną akmenuką paims iš šių laukelių: 2, 4, 9, 10, 15. Vadinasi, iš viso robotas paims 5 akmenukus.
35. Akmenukų mozaika
Čia pateikiama paprasta programavimo kalba – sutartiniais žymenimis nurodomos komandos robotui. Pateiktos keturios programėlės, reikia jas nagrinėti – skaityti ir vykdyti pagal sutartas taisykles. A atveju robotas žengs ant plytelės, padės 3 akmenukus, tada žengs ant kitos plytelės ir padės vieną akmenuką, dar kartą žengs ant naujos plytelės. Taigi 4 akmenukų bokšto negausime. B atveju robotas žengs ant plytelės, padės vieną akmenuką, paskui nepasitraukęs padės dar tris akmenukus ir tada žengs ant naujos plytelės. Taigi B atveju gauname 4 akmenukų bokštą. Reikia nagrinėti toliau, nes gali tikti ir likusios programėlės. C atveju tėra trys akmenukai, tad 4 akmenukų bokšto niekaip negausime. D atvejis panašus į A – tik čia pirma padedamas vienas akmenukas, paskui pažengiama ant naujos plytelės ir tada padedami trys akmenukai.
36. Gražios plytelės
Pateikiama paprasta programavimo kalba – sutartiniais žymenimis nurodomos komandos robotui. Reikia sekti, ar robotas piešia ant tos pačios plytelės, ar žengia ant kitos plytelės. Ant pirmos plytelės robotas nupieš 3 gėlytes, pažengęs ant antros plytelės iš karto nupieš 2 gėlytes ir paskui dar 3, vadinasi, iš viso 5, pažengęs ant trečios plytelės nupieš 1 gėlytę ir paskui dar 3 – iš viso bus nupieštos 4. Matome, kad ant vienos plytelės daugiausiai nupieštos 5 gėlytės.
37. Bebro trobelė
Stogui tinkami rąstai 3, 4, 5, 8, 9. Problema yra su paskutiniu, 11 rąstu. Jo nėra su kuo lyginti, nes daugiau rąstų nebėra. Pagal sąlygas šis rąstas netinka nei grindims, nei stogui, tad tiesiog jį paliekame.
38. Prancūzijos bebras
Paprasčiausia galime imti ir išrašyti besikeičiančių marškinėlių spalvas: mėlyna-balta-raudona-mėlyna-balta-raudona-mėlyna-balta-raudona-mėlyna
Dešimtasis bebriukas dėvės mėlynos spalvos marškinėlius.
Dešimtasis bebriukas dėvės mėlynos spalvos marškinėlius.
39. Bebras ir sūpynės
Sąlygoje matome, kad vienas bebras yra sunkesnis už spausdintuvą, o du bebrai yra tokio pačio svorio kaip motociklas, vadinasi vienas bebras būtų lengvesnis už motociklą. Atsakymas A.
40. Bebras šamanas
Paveikslas turi tenkinti abi pateiktas sąlygas. Atmetimo būdu galime rasti tinkamą atsakymą. Netinka B paveikslas, nes yra lazda. A ir D ne visos sagos susagstytos. Teisingas C.
41. Mėnuleigio kelias
Galima spręsti bent dviem būdais: brėžti mėnuleigio kelią ir stebėti, ar pasitaikys kuris nors iš objektų kelyje arba galima nustatyti visų trijų objektų koordinates (kalno, kraterio ir uolų) ir palyginti su mėnuleigio judėjimo koordinatėmis.
Mėnuleigis sutiks kraterį – jo koordinatės (4, 3).
Mėnuleigis sutiks kraterį – jo koordinatės (4, 3).
42. Bebro žemėlapis
Tilto koordinatės duotos: (5, 6). Vaikai turi mąstyti, ką reiškia „keturiais taškais žemiau“. Problemėlė gali atsirasti, ar skaičiuoti pirmą tašką, kuriame yra tiltas, ar ne. Reikia pateikti analogiškų pavyzdžių: kaip matuojame liniuote? Kai paskaičiuojame keturis taškus žemyn, pataikome ant kelmo, nieko baisaus, nes pasitrauksime į dešinę dviem taškais.
Atsakymas (9, 8)
Atsakymas (9, 8)
43. Kino teatras
Reikia tikrinti kiekvieną užrašą ir žiūrėti, ar kėdė netuščia: randame tuščią vietą – [4, 3]. Tačiau [3, 4] kėdėje sėdi bebriukas, o jo vieta nenurodyta. Klaida aptikta: vietoj [4, 3] turi būti [3, 4].
44. Bebrų namas
Vėlgi galimi keli sprendimo būdai. Vienas trumpiausių – rasti langus, kurie turi keturis gretimus kaimynus, pasirodo, tėra tik du tokie langai: [2, 4] ir [2, 5]. Palyginę matome, kad [2, 5] langas jau atnaujintas. Vadinasi, belieka atnaujinti tik langą [2, 4].
45. Bebras plaukikas
Šis uždavinys – tai maršruto ieškojimas grafe, kuriuo galima pereiti visas jo briaunas po vieną kartą. Jei tokiu maršrutu grįžtama į pradinę viršūnę, jis vadinamas Oilerio ciklu, jei ne – Oilerio keliu. Matematikas Leonardas Oileris įrodė, kad kelias egzistuoja tada ir tik tada, kai lygiai dviejų viršūnių laipsniai yra nelyginiai. Mūsų uždavinyje dvi viršūnės turi po nelyginį skaičių kelių. Bebras pradeda plaukti iš viršūnės, turinčios nelyginį skaičių kelių, vadinasi, turi baigti kairiame viršutiniams name (turi nelyginį skaičių kelių).
Keletas galimų kelių: BCGFHEDA; FHEDACGB; EHFGCADB; DABEHFGC.
Keletas galimų kelių: BCGFHEDA; FHEDACGB; EHFGCADB; DABEHFGC.
46. Drabužių džiovykla
Suprantama, kad stulpas, kuris laiko virves su daugiausia skalbinių, yra naudingiausias ir jį verta stiprinti. Suskaičiuojame, kiek kiekvienas stulpas laiko skalbinių. E stulpas laiko tris virves, ant kurių sukabinta 10 skalbinių.
47. Dantų šepetėliai
Ieva turi didžiausią šepetėlį, vadinasi, kai ji apsikeičia su Lina, tai didžiausias šepetėlis atsiduria tinkamoje vietoje. Ievai su Aine apsikeitus, mažiausias ir vidurinis šepetėliai bus savo vietose. Lieka Benas ir Jonas, turintys ne savo šepetėlius, jiems reikia apsikeisti.
48. Apkeisk
Galime imti kengūras ir skaičiuoti, kiek kortų joms teks įveikti, kol atsidurs eilės kairėje. Vienai kengūrai reikės įveikti (susikeisti) vieną kortą, kitai – dvi kortas. Analogiškai gautume, jei skaičiuotume bebrų keitimus. Taigi iš viso reikės 3 keitimų.
49. Išmanioji varlė
Varlė turi šokinėti taip, kad išvengtų tuščių šuolių, jei tik įmanoma. Varlei prireiks 7 šuolių, kol suės visus vabzdžius.
50. Skalbyklėlė
Pirmasis bebras skalbia 30 min., po to jo drabužiai džiovinami 30 min., per tą laiką antrasis bebras skalbia savo drabužius. Dar 30 min. prireiks antrojo bebro drabužiams išdžiovinti. Abu bebrai sugaiš mažiausiai 90 minučių.
51. Žodžių kodavimas
KOSMOSAS
52. Kodavimo klaida
Reikia atidžiai sekti, kaip skaičiai iš eilės į kurias raides rodo. Perskaitysime žodį SAUSAINUS, vadinasi, 8-oji raidė turi būti I (ne U), ne ten rodo rodyklė.
53. Bebrų kalba
Pradėkime nagrinėti nuo žodžio galo: turime raidžių S ir A kodus, palyginame ir gauname, kad B ir C variantai netinka. A varianto pirmoji raidė žinoma – N, vadinasi, irgi netinka. Belieka D variantas, įsitikiname, kad jis teisingas: pirmosios ir trečiosios raidės kodai vienodi ir jie neduoti, vadinasi, gali būti B raidė.
54. šifras
EIME NAMO
Atkreipiame dėmesį, kad žinutė užkoduota, ją reikia atkoduoti, taigi, raides turime perstumti atvirkščia tvarka negu užkodavome.
Atkreipiame dėmesį, kad žinutė užkoduota, ją reikia atkoduoti, taigi, raides turime perstumti atvirkščia tvarka negu užkodavome.
